
Actor-Critic
- 1 minActor-Critic
参考: 理解Actor-Critic的关键是什么?(附代码及代码分析) - 知乎 (zhihu.com)
什么是AC
PG利用带权重的梯度下降方法更新策略, 而获得权重的方法是蒙特卡罗计算G值
蒙特卡罗需要完成整个过程, 直到最终状态, 才能通过回溯计算G值, 这使得PG的效率被限制.
而改为TD
改为TD还有一个问题需要解决: 在PG中, 我们计算G值, 那么在TD中, 我们应该怎样估算每一步的Q值呢
评估动作的价值,我们称为Q值:它代表了智能体选择这个动作后,一直到最终状态奖励总和的期望;
评估状态的价值,我们称为V值:它代表了智能体在这个状态下,一直到最终状态的奖励总和的期望。
Actor-Critic使用了两个网络: 两个网络有一个共同点: 输入状态S, 但输出策略不同, 一个输出策略负责选择动作, 我们把这个网络称为Actor; 一个输出策略负责计算每个动作的分数, 我们把这个网络称为Critic.
大家可以形象地想象为,Actor是舞台上的舞者,Critic是台下的评委。
Actor在台上跳舞,一开始舞姿并不好看,Critic根据Actor的舞姿打分。Actor通过Critic给出的分数,去学习:如果Critic给的分数高,那么Actor会调整这个动作的输出概率;相反,如果Critic给的分数低,那么就减少这个动作输出的概率。
可以说, AC是TD版本的PG.
TD和MC的比较:
TD算法对蒙地卡罗(MC)进行了改进。 1. 和蒙地卡罗(MC)不同:TD算法只需要走N步。就可以开始回溯更新。 2. 和蒙地卡罗(MC)一样:小猴需要先走N步,每经过一个状态,把奖励记录下来。然后开始回溯。 3. 那么,状态的V值怎么算呢?其实和蒙地卡罗一样,我们就假设N步之后,就到达了最终状态了。 - 假设“最终状态”上我们之前没有走过,所以这个状态上的纸是空白的。这个时候我们就当这个状态为0. - 假设“最终状态”上我们已经走过了,这个状态的V值,就是当前值。然后我们开始回溯。
TD-error
在DQN预估的是Q值, 在AC中的Critic估算的是V值
如果直接用Network估算的Q值作为更新值, 效果会不太好:
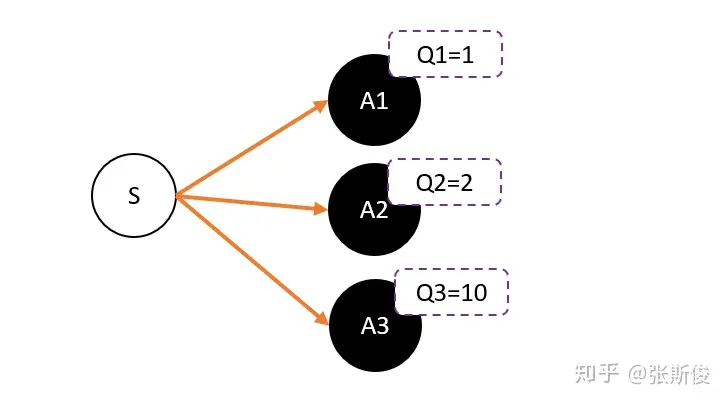
假设我们用Critic网络,预估到S状态下三个动作A1,A2,A3的Q值分别为1,2,10。
但在开始的时候,我们采用平均策略,于是随机到A1。于是我们用策略梯度的带权重方法更新策略,这里的权重就是Q值。
于是策略会更倾向于选择A1,意味着更大概率选择A1。结果A1的概率就持续升高…
这就掉进了正数陷阱。我们明明希望A3能够获得更多的机会,最后却是A1获得最多的机会。
这是为什么呢?
这是因为Q值用于是一个正数,如果权重是一个正数,那么我们相当于提高对应动作的选择的概率。权重越大,我们调整的幅度将会越大。
其实当我们有足够的迭代次数,这个是不用担心这个问题的。因为总会有机会抽中到权重更大的动作,因为权重比较大,抽中一次就能提高很高的概率。
但在强化学习中,往往没有足够的时间让我们去和环境互动。这就会出现由于运气不好,使得一个很好的动作没有被采样到的情况发生。
要解决这个问题,我们可以通过减去一个baseline,令到权重有正有负。而通常这个baseline,我们选取的是权重的平均值。减去平均值之后,值就变成有正有负了。
而Q值的期望(均值)就是V。
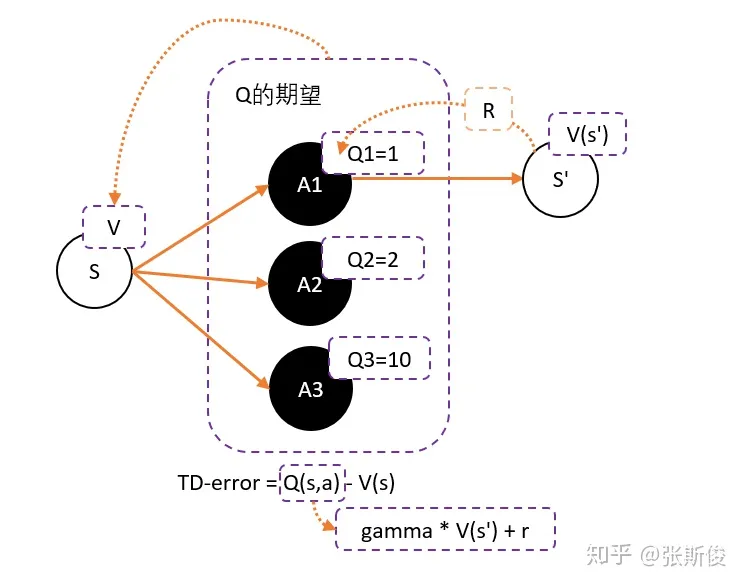
所以我们可以得到更新的权重:Q(s,a)-V(s)
Q(s,a)用gamma * V(s’) + r 来代替,于是整理后就可以得到:
gamma * V(s’) + r - V(s) —— 我们把这个差,叫做TD-error
Critic的任务就是让TD-error尽量小。然后TD-error给Actor做更新。
TD-Error的注意事项
-
为了避免正数陷阱,我们希望Actor的更新权重有正有负。因此,我们把Q值减去他们的均值V。有:Q(s,a)-V(s)
-
为了避免需要预估V值和Q值,我们希望把Q和V统一;由于Q(s,a) = gamma * V(s’) + r - V(s)。所以我们得到TD-error公式: TD-error = gamma * V(s’) + r - V(s)
-
TD-error就是Actor更新策略时候,带权重更新中的权重值;
-
现在Critic不再需要预估Q,而是预估V。而根据马可洛夫链所学,我们知道TD-error就是Critic网络需要的loss,也就是说,Critic函数需要最小化TD-error。
Actor-Critic算法
-
定义两个network:Actor 和 Critic
-
j进行N次更新。
-
- 从状态s开始,执行动作a,得到奖励r,进入状态s’
- 记录的数据。
- 把输入到Critic,根据公式: TD-error = gamma * V(s’) + r - V(s) 求 TD-error,并缩小TD-error
- 把输入到Actor,计算策略分布 。

Actor的loss解释
TD 目标(td_target)和 TD 误差(td_error)
-
td_target = reward + (1 - done) * gamma * next_state_value:
- 这是时间差分目标(Temporal Difference Target)。它表示在当前状态 sts_tst 采取动作 ata_tat 后的预期回报。
reward是当前时间步获得的即时奖励。(1 - done)确保当一个 episode 结束时,不考虑未来状态的价值。gamma是折扣因子,用于平衡即时奖励和未来奖励。next_state_value是 Critic 估计的下一个状态 st+1s_{t+1}st+1 的价值。
-
td_error = td_target - state_value:
- 这是 TD 误差(Temporal Difference Error)。它表示当前 Critic 估计的值与实际 TD 目标之间的差异。
state_value是 Critic 估计的当前状态 sts_tst 的价值。
获取所采取动作的概率
-
action_prob = tf.gather_nd(action_probs, [[0, action]]):
- 这是 Actor 根据当前策略选择动作 ata_tat 的概率。
action_probs是 Actor 输出的所有动作的概率分布。tf.gather_nd提取了 Actor 对应于所采取动作 ata_tat 的概率值。
计算 Actor 的损失
-
actor_loss = -tf.math.log(action_prob) * td_error:
- 这是 Actor 的损失函数,用于更新策略参数。
tf.math.log(action_prob)是所采取动作 ata_tat 的对数概率。对数概率的负值用于最大化所采取动作的概率。td_error是 Critic 提供的 TD 误差,表示当前策略选择的动作与理想动作之间的差异。- 通过最小化
-tf.math.log(action_prob) * td_error,我们实际上在最大化tf.math.log(action_prob) * td_error。这意味着如果 TD 误差是正的(动作好于预期),我们增加该动作的概率;如果 TD 误差是负的(动作差于预期),我们减少该动作的概率。